Prestressed Reinforced Continuous Rigid Frame Bridge
- original innovation
- Open Access
- Published:
Seismic cracking mechanism and control for pre-stressed concrete box girders of continuous rigid-frame bridges: Miaoziping bridge in Wenchuan earthquake as an example
Advances in Bridge Engineering volume 2, Article number:17 (2021) Cite this article
Abstract
The box girder of the Miaoziping Bridge, a three-span prestressed concrete continuous rigid-frame bridge, suffered a serious crack in its box section's web near the 1/6 to 1/2 length of the side span and the middle-span length of 1/4 to 3/4, as a result of the 2008 Wenchuan earthquake, which also caused large lateral residual displacements at both ends of the side span. In this study, eight strong-motion records near the bridge site and two other records (El Centro and Taft) are selected as inputs for time-history analysis of the bridge. The cantilever construction process and initial stress of the box girder are considered in a bridge model for seismic numerical simulation. Further, the simulation results are compared with the actual earthquake damage. The cracking mechanism, influencing factors and control of the girder crack damage are discussed. The high-stress zones of the box girder agree with the seismic damage observed, even various seismic inputs are considered. The findings reveal that the maximum (principal) tensile stress of the girder exceeds the tensile strength of the concrete under the seismic excitations, and cracks occur. Under various input directions of ground motions, the proportion of the main girder stresses induced by the earthquake shows differences. After the failure of the shear keys in the transverse direction of the bridge, the stresses of the girder decrease in the mid-span. However, the beams at both ends of the side spans revealed large lateral displacements. Considering that the uplift of the beam ends, stress and axial torque of the girder's side span are greatly reduced. Setting bi-directional friction pendulum bearings on the transition pier is an effective damping measure to control web cracking of the mid-span and lateral drifts of the beam ends.
Introduction
In the western regions of China with high seismic risks, many pre-stressed concrete continuous rigid-frame bridges (PCCR) with high piers and long spans have been constructed over the last two decades (Jia et al. 2013; Wang et al. 2019). At present, significant research has been carried out on the seismic performance of the PCCR with high piers. In addition to the discussion of the seismic ductility (Sun et al. 2019; Guan et al. 2017), this research also includes the topography effects, and multi-dimensional earthquake excitations (Shrestha et al. 2015; Li et al. 2018) and collapse analysis (Zong et al. 2016). Xu et al. (2020) and Lin et al. (2020a, b) also carried out shaking table tests on seismic responses for PCCR. For these studies, it is generally believed that the earthquake damage will be concentrated on the bridge piers, and the main girder will keep elastic during an earthquake. It should be noted that the earthquake action on the main girders of the pre-stressed concrete continuous rigid-frame bridge is often ignored in practice design.
A multi-span PCCR with high piers and long span, although piers have a certain flexibility, still has the same mechanical properties as those of rigid plane frames; when the horizontal force is applied to the frame in the plane, the beam will demonstrate resisting forces. Because the main girder and the pier are rigid together in a PCCR, instead of the bearings are used between them like the simply supported bridge or continuous bridge. The girder will certainly resist the seismic force together with the pier, especially for an earthquake in the longitudinal and vertical directions of the bridge. If the ground motions get larger, the main girder with prestressed reinforced concrete (PRC) may crack or even yield in a strong earthquake.
The 2008 Ms. 8.0 Wenchuan earthquake resulted in obvious damage to the Miaoziping Bridge, which was located less than 15 km from the earthquake's epicenter. The main bridge and the approach bridge were both damaged. The girder had been fallen in the tenth span for the approach bridge, which was simply supported. Further, the cracking was under water at the foot of the No.5 main pier for the main bridge which is a rigid frame bridge. It is worth noting that the box girder of the main bridge experienced a serious cracking phenomenon; the side span had a large lateral residual displacement as well. These damages are hardly seen in previous bridge damage in earthquakes (Kawashima et al. 2009; Chen et al. 2012). It is also the first domestic case of earthquake damage of a large-span PCCR with above 100 m high piers in recent years, which indicates that more focus is required on the damage mechanism of the bridge.
After the 2008 Wenchuan earthquake, field investigations and research have been carried out for the Miaoziping Bridge. Chen et al. (2018) analyzed the seismic vulnerability on the main bridge. Deng et al. (2019) discussed the water-pier coupling effect of the main bridge and the impact of the longitudinal collision of girders on the piers. All of the research focuse on the response of piers of the Miaoziping Bridge; only Yang et al. (2012) discussed the seismic damage of the main girders of the Miaoziping Bridge. It is considered that the tensile stress at the bottom plate of the box girder exceed the tensile strength of the concrete in the closure section of the side span of the bridge during the earthquake.
Generally speaking, for the Miaoziping Bridge, there is still a lack of comparative analysis of the cracking of the girder from real seismic damage by numerical simulation. The cracking mechanism, influencing factors, and control of girder seismic damage have not been revealed clearly. Based on the actual seismic damage of the box girder of the Miaoziping Bridge in the 2008 Wenchuan earthquake, the initial stress along the section of the box girder is obtained by considering the construction process with the model developed by Midas Civil software; then, the time history analysis with the records from the 2008 Wenchuan earthquake near the bridge site is carried out. The cracking mechanism of the box girder is discussed by the maximum (principal) tensile or maximum (principal) compressive stress of a girder's section under the seismic action. The contributions of transverse, longitudinal and vertical ground motions to the main girder stress are quantified. The influence of the shear keys failure and the beam end uplift on the cracking of the main girder is discussed. The seismic mitigation and isolation measures for the main girder cracking are proposed.
Miaoziping bridge and girder seismic damage
The Miaoziping Bridge was located 15 km upstream of the Zipingpu Reservoir Dam in Dujiangyan, Sichuan Province. The main bridge was a prestressed concrete continuous rigid frame bridge with spans of 125 m, 220 m and 125 m. The main bridge girder was designed by 3D prestressed systems with single-box and single-chamber section (Fig. 1). The box girder was designed according to a full-pre-stressed structure which means the tensile stress was not allowed for the bridge operation. The piers 4 and 5 had a rectangular hollow section, and piers 3 and 6 had a double-column thin-wall hollow section. Pile group foundations were designed and supported by the stratum or bedrock. The girder was cast by C60 concrete, while the piers were cast by C40 concrete. The two-way movable basin rubber bearings (GPZ10SX) were installed on the top of the piers on each side-span of the bridge; their vertical bearing capacity was 10,000 kN; the longitudinal displacement capacity was 20 cm and the lateral displacement capacity was 4 cm. The shear keys (restraint blocks) were at the end of the cap beam of the pier, which has been marked in Fig. 1 (Detail 1).
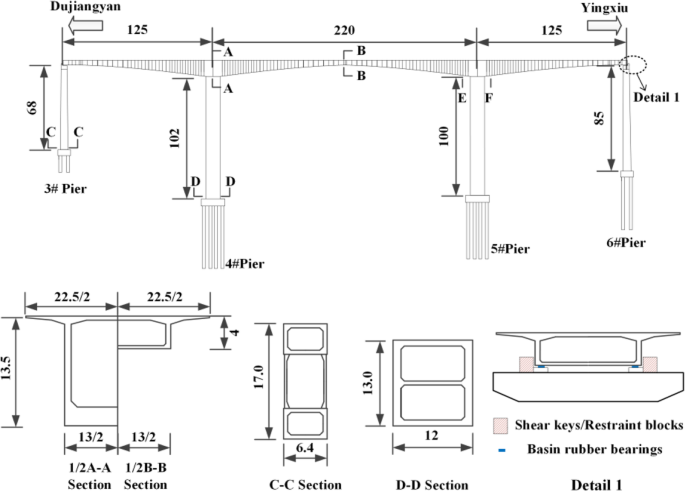
Arrangement of bridge span and cross-section (unit: m)
Seismic design of the bridge is based on the seismic precautionary intensity of VII degrees with the PGA equaling to 0.1 g. The seismic performance is evaluated with a PGA of 0.24 g and the probability of exceedance of 2% in 100 years. Some common engineering problems in the long-term service of the PCCR are reported, such as, mid-span deflection, web cracking and prestress loss of the main girders (Huang et al. 2018). When the 2008 Wenchuan earthquake occurred, the main section of the Miaoziping Bridge had just been completed; only the expansion joints had not been installed, and the main girder had no initial damage and cracking.
Figure 2 shows the relative position of the bridge site, earthquake faults, and record stations. Table 1 shows the information of eight record stations near the bridge site. It can be seen that the bridge site is located between the two faults, and the distance from the Beichuan-Yingxiu fault is less than 6 km. The longitudinal direction of the bridge is 50° to the north by west, and the intersection angle with the Beichuan-Yingxiu fault is about 40°. The peak ground accelerations (PGAs) of the stations near the fault, such as Wenchuan Wolong (WCW) Station, Mianzhu Qingping (MZQ) Station and Shifang Bajiao Station (SFB), are relatively large. The MZQ station which is close to the fault surface rupture is located between the two faults as the same as the bridge does. Figure 3 shows the acceleration response spectra of eight strong motion records.
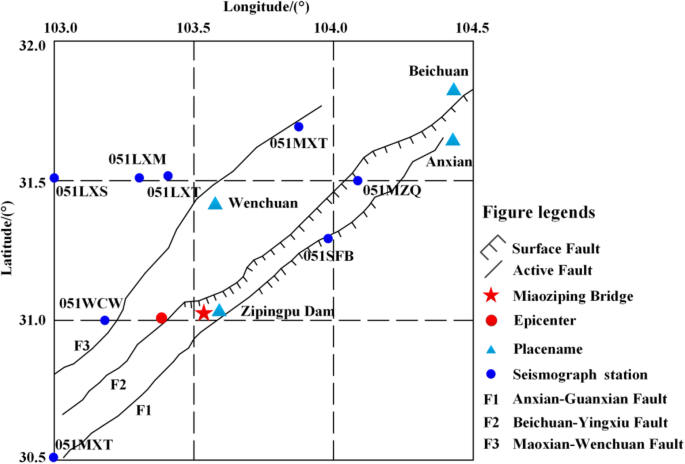
Bridge, fault, and earthquake record station
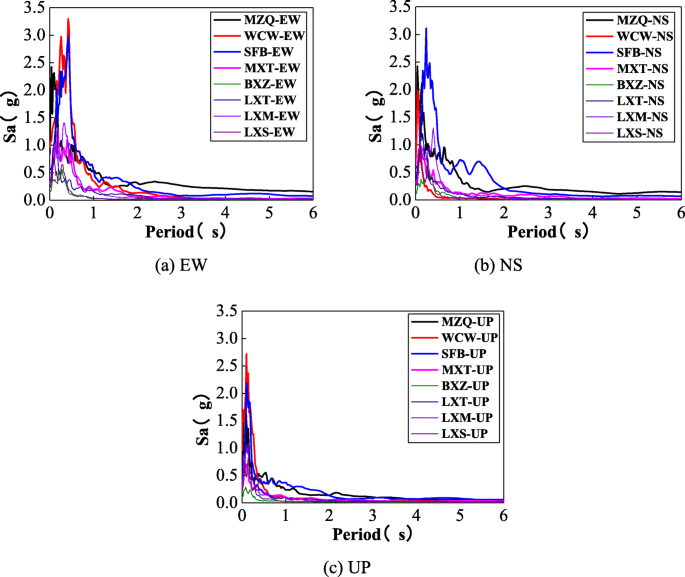
Acceleration response spectra (damping ratio 5%)
Figures 4 and 5 show seismic damage pictures and longitudinal crack distribution along the bridge girder during the 2008 Wenchuan earthquake. The cracks in the web of girder's section are mainly inclined cracks, which developed from the bottom to the top of the section. Distribution of cracks along the bridge in the upstream and downstream sides is nearly the same. The cracks are mainly located in the areas of the 1/6–1/2 side-span length and 1/4–3/4 mid-span length. The cracks on the bottom plate of the section are mainly concentrated in the closure section in the construction process. They are either in the mid-span or in the side-span of the bridge. The cracking is also found in two to three adjacent sections of the closure section. For closure sections, the concrete in the mid-span and side-span appears to have failed in the local part underneath the girder. Furthermore, there are traces of extrusion and spalling of the concrete. This is due to the pavement has been completed before the earthquake, the crack on the top plate of the box section is not seen clearly.
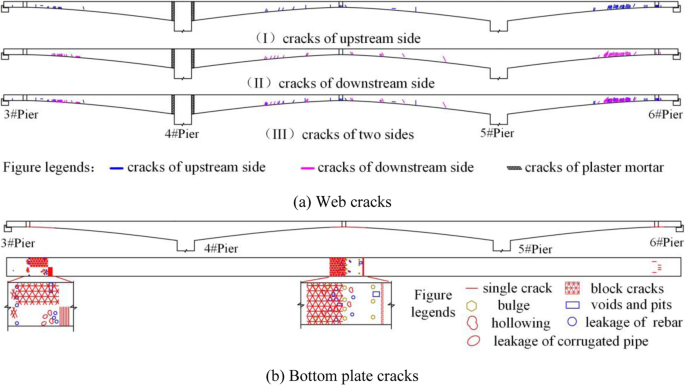
The distribution of longitudinal cracks of the girder

Partial seismic damage pictures of the main girder (Chen et al. 2012)
Finite element model
Finite element modeling is performed using Midas Civil software and the main girder is set with 162 beam elements. Because the pile foundations enter the rock layer to a certain depth and the cover layer thickness is 10 m, soil-structure interaction is not considered. The half-span loads of the adjacent approach bridges are simplified as the concentrated mass, which is applied on the top of each side-span pier.
The main bridge was constructed by the cantilever cast method at the site. In the first step, the initial stress under the dead load for the girder section is present according to the construction process. The numerical simulation for the construction process includes applying a hanging basket, wet weight acting, deck pavement loading, and prestressed loading with 402 prestressing tendons (Fig. 6). The bearings are simulated by setting four elastic connection elements. Due to the spacing between the main girder and the shear keys is only 10 cm (including 7 cm thick rubber block) in the transverse direction of the bridge, the transverse displacement between the girder and the pier is constrained. In addition, constraint in the longitudinal direction of the bridge is released with the friction factor μ equaling to zero. (Fig. 7).

Prestressing tendons in the model
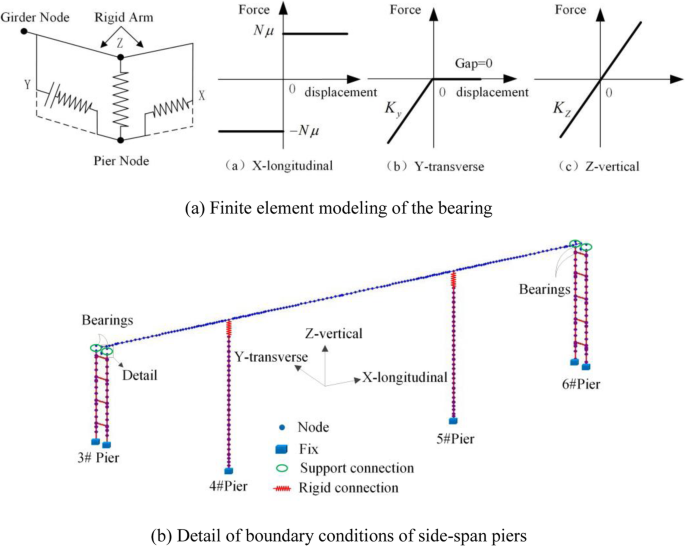
Modeling and boundary conditions of the bridge
The E and F points were stress-monitoring points of the main girder during bridge construction at the site (see Fig. 1). These points were also at the top of the pier 5 under the cantilever construction process of the bridge. Ma (2008) carried out on-site construction monitoring of the main bridge and obtained the value of the bottom plate stress of the E and F points of the main girder. Figure 8 shows a comparison between the simulation results of this paper and the field measurement results. It can be seen that the simulation results are in good agreement with the measured stress trends. The simulation results in this paper are minor smaller than the actual monitoring data during the cantilever casting process, but the stress at the closure stage (completion status of the bridge construction) is less than 1 MPa from the actual monitoring data. It illustrates that the theoretical calculations are basically in line with the actual construction process and verifies the accuracy of the initial stress of the main girder of the bridge.
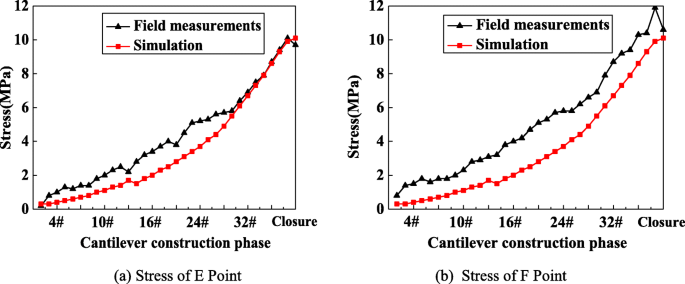
Comparison of simulation and actual measured stress
Figure 9 shows the initial (principal compressive or tensile) stress of the box section of the girder after completion of the bridge. The web stress is taken from the point where chamfer of the web plate and the bottom plate intersects. It can be seen that all sections of the box girder are basically in a full compression state. In addition, there are large peak values at the girder's sections near the piers. It should be noted that they may be influenced by the piers. So the calculated stress values at these positions may not be reliable (as shown below).
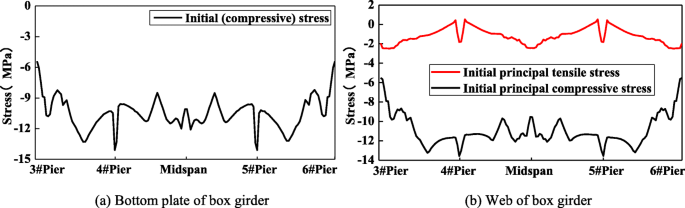
Initial stress of box girder section
The vibration modes of the main bridge are analyzed. The results show that five of the first ten modes are mainly dominated by the transverse vibration of the girder. Fig. 10 shows the first four vibration modes of the Miaoziping Bridge.
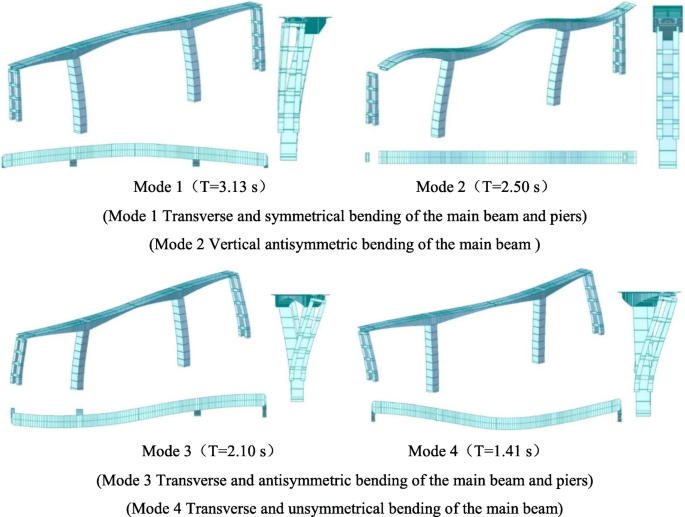
First four vibration mode of the Miaoziping Bridge
The soil of the site of the Miaoziping Bridge is hard. The El Centro record and the Taft record are also mainly suitable for medium/hard site soil conditions, which are widely used in the literature for the time history analysis. To have a better understanding of the uncertainty effect of ground motion input on the bridge damage responses, the El Centro record and the Taft record, together with other eight seismic records in 2008 Wenchuan earthquake are used in time history analysis (Table 1). The records are divided into two groups: (i) original ground motion records without amplitude modification; (ii) ground motion records with modified PGAs of 0.55 g, 0.55 g and 0.37 g for NS, EW and vertical components, respectively. These records are as the same as those for the seismic damage analysis of the Zipingpu Dam by Kong et al. (2012). The authors demonstrated that the records of the Maoxian Diban Station (MXT) after amplitude scaling could be used as the ground motion input for the Zipingpu Dam (about 2.9 km from the bridge site) in the 2008 Wenchuan earthquake.
Considering the longitudinal direction of the bridge is 50o to the north by west, coordinate rotation is carried out for two horizontal ground-motion accelerations of EW and NS components, as shown in Eq. (1):
$$ {\displaystyle \begin{array}{l}{X}_{\parallel }={X}_{EW}\cdot \sin \left(\theta \right)+{X}_{NS}\cdot \cos \left(\theta \right)\\ {}{X}_{\perp }={X}_{EW}\cdot \cos \left(\theta \right)-{X}_{NS}\cdot \sin \left(\theta \right)\end{array}} $$
(1)
where θ is the angle between the longitudinal direction of the bridge and EW direction, taking 50°, and X ∥ and Y ⊥ are the horizontal components of ground motions for the longitudinal and transverse directions of the bridge.
Main girder cracking damage and numerical simulation
Time-history analysis for the bridge is carried out considering the initial internal force of the dead load under the 10 groups of ground motions. Due to the limited length of the paper, only the stress responses of the main girder under the ground motions with the scaled amplitude are presented. The difference between the actual seismic damage and stress under the El Centro ground motion is significant. This part is not listed here.
Comparison between the actual seismic damage of the main girder and the simulation results is shown in Figs. 11 and 12. The solid lines represent the maximum (principal) tensile stress; the dotted lines represent the maximum (principal) compressive stress, and the thickened real lines and dotted lines represent the records with larger stress responses.
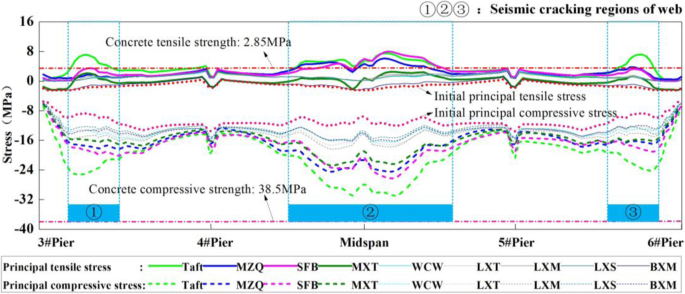
Comparison between the monitored seismic damage and numerical simulation of the web
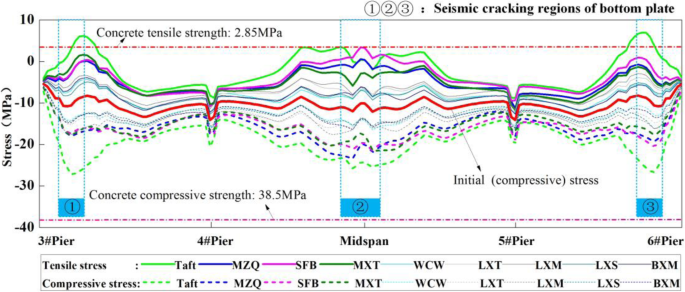
Comparison between the monitored seismic damage and numerical simulation of the bottom plate
The stress response trends of different records are almost the same, but the magnitudes are different. The stress responses of LXT, LXM, LXS, MXM, and WCW have relatively small values, which are different from the actual earthquake damage of the bridge. Under the input of Taft, MZQ, SFB and MXT, the values of the stress are in good agreement with the earthquake damage of the girder. It should be noted that the cracking damage areas are consistent with the maximum tensile zones and compressive stress zones obtained by the numerical simulation in cases with various input excitations.
Based on the spatial location of record stations, bridge site, and faults, the stress responses of the main girder are discussed in detail by taking the ground motion of MZQ as an example. For middle span, the principal tensile stress of the web, at the girder's section 15 m away from the closure section of the middle span (close to the side of the pier 5), is 8 MPa. The value significantly exceeds the standard value of the axial tensile strength of C60 concrete (2.85 MPa). The main compressive stress is 24 MPa, which is close to the standard value of the axial compressive strength of C60 concrete (38.5 MPa). For two side-spans, the principal tensile and the principal compressive stress values of the webs are relatively small. The maximum principal tensile and compressive stress values reach 3.5 MPa and 17 MPa, respectively.
The numerical simulation shows that the tensile stress of the bottom plate reaches 2 MPa in the mid-span, which is close to the standard value of concrete tensile stress. The compressive stress increases by 15 MPa compared with the initial stress and reach 24 MPa, which is close to the standard value of concrete's compressive strength. The tensile stress and compressive stress of the side span are relatively small. The maximum tensile stress is less than 1 MPa, and the maximum compressive stress increases about 9 MPa compared with the initial stress, reaching 17 MPa.
In a word, in the web and the bottom plate of the box section for the bridge girder, the actual crack zones are closer to the high-tensile-stress distributed areas and high-compressive-stress distributed areas, which are obtained by numerical simulation. To further study the cracking mechanism of large-span rigid-frame bridges with high piers with consideration of the cracking damage of the girder with the box section, another two rigid-frame bridges with different pier heights and spans are taken as examples (Tong et al. 2020). The findings are consistent with the earthquake damage of Miaoziping Bridge. The height of piers has the main influence on the stress of the main girders of the rigid-frame bridge, and the span may be the secondary influence factor. The main piers heights and spans of the bridge are larger, the (principle) tensile and (principle) compressive stress are greater. It reveals that the analysis results of this article are universal.
Effect of unidirectional ground motion
To demonstrate the effect of the unidirectional ground motion on the cracking of the girder, the bridge is subjected by vertical component, transverse component X ⊥, and longitudinal component X ∥ separately for time-history analysis. The records are set to the same acceleration magnitudes, 0.55 g horizontally and 0.37 g vertically.
Under the excitations of Taft, MZQ, SFB, and MXT records, the seismic responses of the bridge are analyzed. Stress increments of the girder sections under the un-directional ground motion input and the three-directional input of each record are calculated, respectively. Then the ratio of the two "stress increments" is determined. After that, the average value form the four records is taken as the contribution in each direction for the three-directional ground motion input (Eq. 2). Finally, normalization is done because the maximum responses are not synchronized. Among them, the stress increment is the difference between the section stress value under the seismic excitation and the initial stress at the corresponding position, as shown in Eqs. (2) and (3):
$$ {P}_i=\left(\frac{\Delta {\sigma}_{Taft-i}}{\Delta {\sigma}_{Taft\left(\mathrm{three}\hbox{-} \mathrm{direction}\right)}}+\frac{\Delta {\sigma}_{MZQ-i}}{\Delta {\sigma}_{MZQ\left(\mathrm{three}\hbox{-} \mathrm{direction}\right)}}+\frac{\Delta {\sigma}_{SFB-i}}{\Delta {\sigma}_{SFB\left(\mathrm{three}\hbox{-} \mathrm{direction}\right)}}+\frac{\Delta {\sigma}_{MXT-i}}{\Delta {\sigma}_{MXT\left(\mathrm{three}\hbox{-} \mathrm{direction}\right)}}\right)/4, $$
(2)
$$ {P}_i^{\hbox{'}}=\frac{P_i}{P_i+{P}_j+{P}_k}, $$
(3)
Where i, j, k = directions of the ground motion input (i.e. the vertical ground motion, the transverse ground motion X ⊥ , and the longitudinal ground motion X ∥ ).
Δσ wave −i = Stress increment of girder section under the un-directional ground motion of i direction.
Δσ wave(three ‐ direction)= Stress increment of girder section under the three-dimensional ground motion.
P i = Average ratio of stress increment of the ground motion input in the i direction to that in the three-directions.
P i = Normalized ratio of stress increment of the ground motion input in the i direction to the stress increment of the three-directional ground motion.
Figure 13 shows the seismic damage regions of the web and the stress increment proportion of ground motion in three directions (the map of the percentage accumulation area is used). The longitudinal direction's proportion contribution to the principal tensile stress increment of the full-bridge girder is between 30% and 40%, especially in the seismic damage regions of the left side-span (Fig. 13a). The transverse direction's proportion contribution to the principal tensile stress is between 30% and 35%, especially in the mid-span. The vertical direction's proportion is about 30% of the whole and is relatively small in the mid-span.
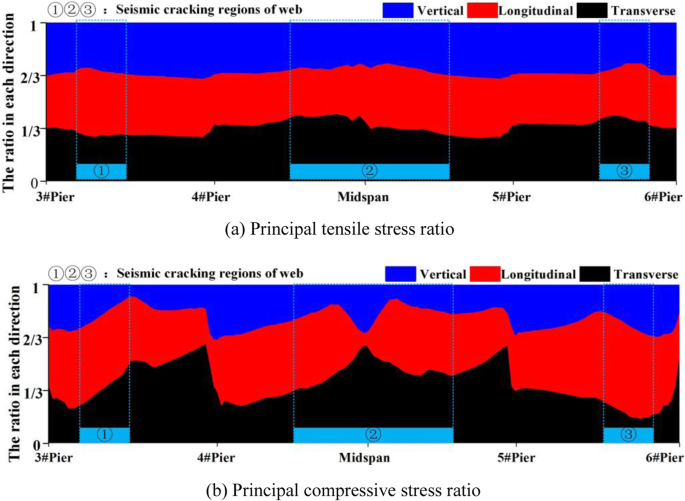
Proportion of web principal stress under different ground-motion directions
In the seismic damage regions of the left side-span, the longitudinal direction's proportion contribution to the principal compressive stress is 45% - 50%, 55% for the right side-span of high-stress area, and about 45% for the mid-span high-stress area (Fig. 13b, excluding the closure section in the mid-span). In the seismic damage regions of the side span, the transverse direction's proportion of the principal compressive stress is between 15% and 35%, and that in the seismic damage regions of the mid-span is between 30% and 60%; it reaches 60% in the closure section of the mid-span. The vertical direction's proportion of the principal compressive stress is less than 30%.
Figure 14 shows the seismic damage regions of the bottom plate and the stress increment proportion of ground motion in three different directions. The longitudinal direction's proportion of the tensile stress increment of the full bridge girder is between 50% and 60%, especially in the seismic damage regions of the right side-span (Fig. 14a). In the mid-span closure section, however, the proportion is the smallest, only about 4%. The transverse direction's proportion of the tensile stress is between 15% and 35%, which accounts for the largest proportion in mid-span closure section (reaching 70%). The vertical direction's proportion of the tensile stress about 30% of the whole.
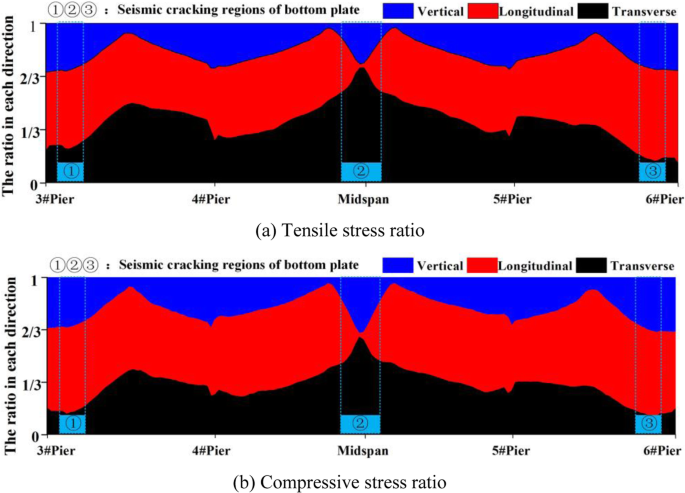
Proportion of bottom plate stress under different ground-motion directions
In the seismic damage regions of the left side-span and right side-span, the longitudinal direction's proportion of the compressive stress is about 50%, 5% - 30% for the mid-span (Fig. 14b, excluding the closure section). In the seismic damage regions of the side span, the transverse direction's proportion of the compressive stress is between 15% and 35%. The transverse direction's proportion is between 30% and 60% in the seismic damage regions of the mid-span, and it reaches 60% in the closure section of the mid-span. The vertical direction's proportion of the compressive stress is less than 35%, and the closure section in the mid-span accounts for the largest proportion of 35%.
Among the three directions for earthquake excitation, the longitudinal ground motion causes a larger bending moment of the section in the side span of the bridge, so it accounts for a relatively large amount, especially for the principal compressive stress. On the whole, the proportion of principal tensile stresses of the web in the longitudinal, transverse, and vertical directions are average. Special attention should be paid to the effect of longitudinal ground motion on the web-crushing damage by the compress stress of the side span and mid-span. The bending moment of the bottom plate of the closure section in the mid-span caused by the longitudinal ground motion can basically be small, so the stress of the bottom plate in the mid-span is not remarkable. As a whole, when the stress of the girder for the frame bridge is considered, it is necessary to focus on the effect of the longitudinal ground motion on the side-span and the effect of transverse ground motion on the mid-span; thus, the 3D earthquake excitations must be adopted.
Effect of shear keys damage and beam end uplift
The seismic damage at the beam ends for the two side-spans of the Miaoziping Bridge is shown in Fig. 15. From the appearance, the development process of seismic damage can be guessed. When the span of the side span of the PCCR is large, the beam end of the side span is prone to large lateral displacement under the transverse ground motion. It will lead to bearing damage (Fig. 15a), and beam end collision with the lateral shear keys. After the shear keys fail (Fig. 15b), there is no lateral restraint at the beam end; thus, a greater displacement response will happen.

Seismic damage of beam-end at the transition pier (image by Prof. Xun Guo)
For a three-span frame bridge like the Miaoziping Bridge, if the ratio of the side-span mass to the middle-span mass is relatively small or the vertical seismic action is large, the bearings will easily lose tension limit in the vertical direction and become compression-only bearings. Meanwhile, the girder beam is easy to slap vertically with the top of the transition pier (Fig. 15.c). For example, Katsaras et al. (2009), Wilson et al. (2015), and Ucak et al. (2014) found a possibility of vertical uplift at the beam end of the concrete continuous bridges.
Whether different boundary conditions will affect the simulation results or cognition of the final seismic damage is the focus of this section. According to the actual earthquake damage of bearings and shear keys at the transition piers, the influences of earthquake damage on the bridge are discussed in three boundary conditions: (1) with shear keys, the lateral responses at the end of the girder are elastically restrained, and bearings and shear keys are not damaged (Fig. 7b); (2) without shear keys: shear keys are damaged, so the bridge lateral responses are not restrained at the end of the girder; bearings are not damaged as well (Fig. 16a); (3) uplift of the beam ends, shear keys are not damaged and can restrain the lateral displacement response. The bearings are damaged and the nonlinear gap connections are used to simulation the compression-only (uplift) behaviors in vertical direction of the beam ends (Fig. 16b).
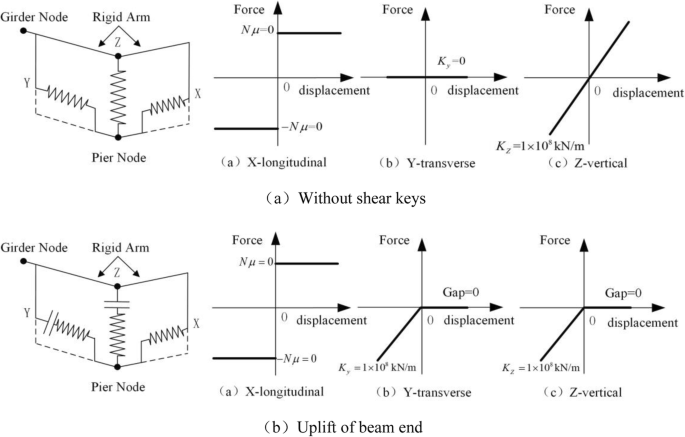
Simulation of boundary conditions of bearings at the top of the transition piers
All constraints in the longitudinal direction of bearings of the bridge are released. Taking the MZQ and SFB records as the seismic inputs; for that, simulation results are highly consistent with the real seismic damage. The impacts of the damage of the shear keys and the compression-only behavior (uplift) of the beam ends on the section stress, torque force, collision, and displacement of beam ends are analyzed.
Section stress of the girder
Figures 17 and 18 show the stress response of the girder under different boundary conditions. On the whole, the girder stress changes after the shear keys' damage and the beam end uplift, but the high stress zones are consistent with the real seismic cracking distribution of the girder. The general trend of stress response remains unchanged, which further confirms the credibility of the numerical simulation of the seismic damage of the Miaoziping Bridge in this paper.
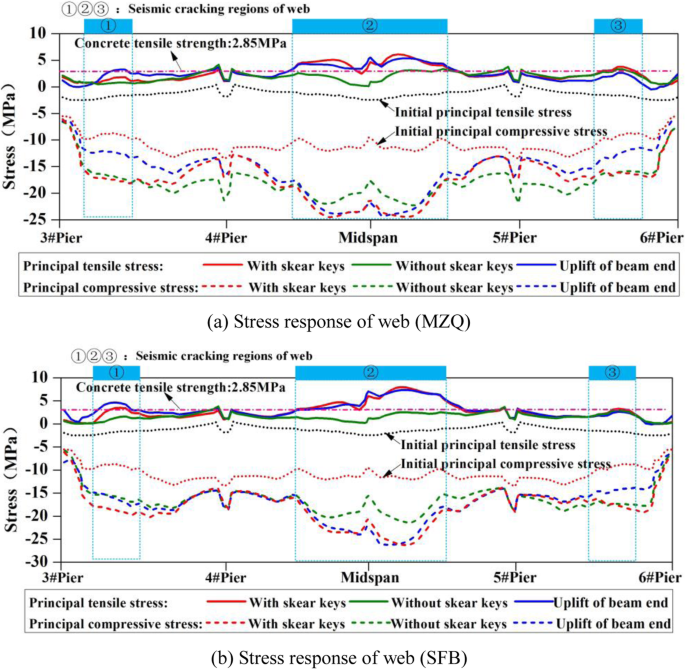
Stress response of web under different boundary conditions
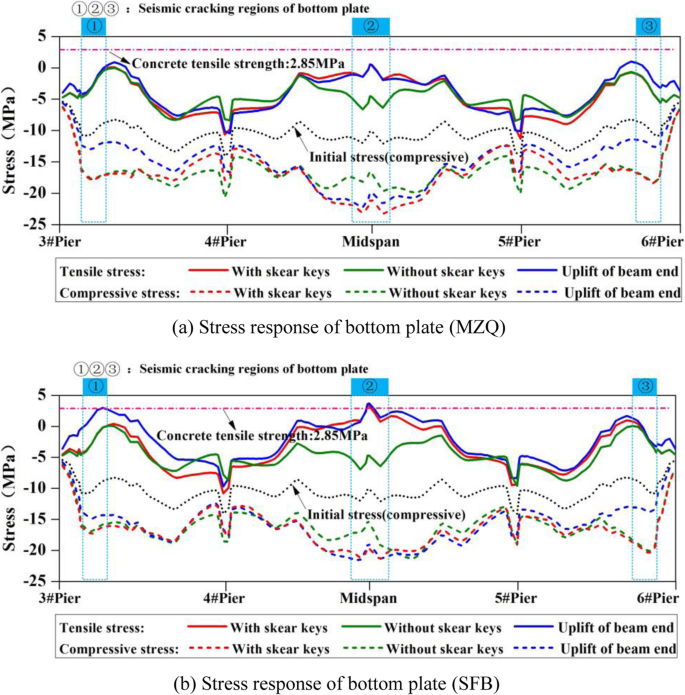
Stress response of bottom plate under different boundary conditions
After the damage of the shear keys, the stress changes of the web and the bottom plate of the sections are basically the same, and the changes are mainly reflected in the areas near the main pier and mid-span, especially the latter. The (principal) tensile and (principal) compressive stresses of the web and the bottom plate in the mid-span area are reduced to some extents, but the stresses of the girder near the main pier increase to a certain extent.
The principal tensile and principal compressive stresses of the web near the mid-span are reduced by 3 MPa (4 MPa) and 2.5 MPa (4 MPa), respectively. Here, the values of the stresses under MZQ ground motion are given, and the values in brackets represent the stress under SFB ground motion. The principal tensile and compressive stresses of the bottom plate in the mid-span are reduced by about 5 MPa (8 MPa) and 4 MPa (3.5 MPa) respectively. The principal tensile and principal compressive stresses of the web near the main pier increase by 0.3 MPa (0.2 MPa) and 4 MPa (0 MPa) respectively; the principal tensile and principal compressive stresses of the bottom plate near the main pier increase by about 2 MPa (1 MPa) and 3 MPa (0.5 MPa).
After the failure of the shear keys, the beam ends of the side span will cause large lateral displacement responses under the transverse ground motion. Due to the large transverse stiffness of the girder at the main pier, the bending moment will get larger, which makes the (principal) tensile and (principal) compressive stresses increase. On the contrary, the transverse bending moment transferred to the mid-span decreases, which leads to the decrease of the (principal) tensile stress and (principal) compressive stress.
Considering the uplift behaviors of the beam ends, the stress changes trends of the web and the bottom plate of the box section are almost the same, and the changes are mainly reflected in the side span; further, they have little influence on the mid-span. The (principal) tensile stress of the web and bottom plate in the side-span area are increased, but the (principal) compressive stress of the web and bottom plate are decreased. The results show that the tensile stress of the bottom plate increases by 1.5 MPa (3 MPa); the compressive stress decreases by 5 MPa (6.5 MPa); the principal tensile stress of web increases by 1.5 MPa (1 MPa), and the principal compressive stress decreases by about 6 MPa (4.5 MPa). The analysis shows that, after uplift of the beam ends, the bending moments of the beam ends of the side span are released and lead to increasing of the (principal) tensile stress and decreasing of the (principal) compressive stress in the side span.
Torque force of the girder
The the post-earthquake investigation of the Miaoziping Bridge after the 2008 Wenchuan earthquake revealed found that the box section of the main girder had local cracks at the chamfering of the diaphragm, which indicated that the main girder had experienced a certain torque around the longitudinal axis of the bridge. Figure 19 shows the axial torque of the main girder under various boundary conditions. When the shear keys are damaged, the torque forces at both beam ends of the side span are the greatest, and the torque in the mid-span increases to a certain extent. Considering uplift of the beam ends, the torque of beam ends of the side span are the minimum.
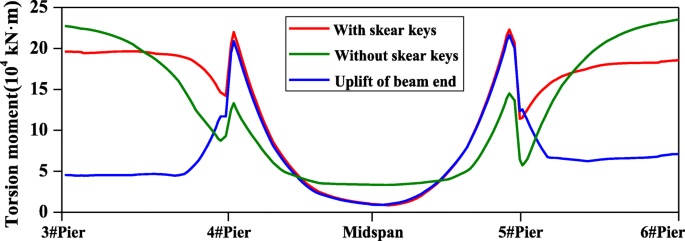
Torque moment of main beam around longitudinal axis (MZQ)
The failure of the shear keys has no significant effect on the axial torque of the girder. Considering uplift of the beam ends, the unilateral bearing can uplift to release the restraint force under the action of the axial torque, which leads to the reduction of the torque at the beam ends of the side span, which can reduce about 75%. Because the main pier and the beam are consolidated together, the torque force can hardly be transferred from the side span to the mid-span, and cause a minor difference of the torque in the mid-span under the various boundary conditions.
Displacement and collision force of the beam ends
Figure 20 shows that the residual lateral displacements of the side-spans of the Miaoziping Bridge were obvious in the 2008 Wenchuan earthquake. The girder's lateral displacement at the No. 3 Transition Pier was 43 cm, and 36 cm at the No. 6 Transition Pier. The girder displacements at the No. 4 Main Pier and No. 5 Main Pier were obviously smaller than those at the transition pier, but they were not the same, which lead to the lateral rigid body displacements and rotation of the bridge. Because the transverse displacement responses of the girder in the mid-span were mainly controlled by the No. 4 Main Pier and the No. 5 Main Pier, the lateral residual displacements were much smaller than that of the side-span (Chen et al. 2012).

Residual lateral displacement of the main girder in the 2008 Wenchuan earthquake (Chen et al. 2012)
Figure 21 shows the simulation model of the girder transverse drift responses. After damage of the shear keys, the beam ends of the side span show large lateral displacements. The maximum transverse displacement response of the girder under different ground motions is shown in Fig. 22. The transverse displacement responses of the beam ends under MZQ ground motion are both about 95 cm, and the transverse displacement responses under Taft ground motion and SFB ground motion are slightly greater than the post-earthquake residual displacement (43 cm). By comparison, it is found that the lineshape of the maximum transverse displacement responses is more consistent with the lineshape of the residual displacement after the earthquake.
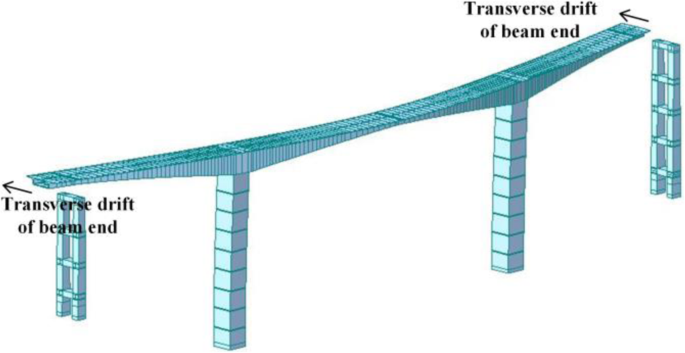
Simulation diagram of main beam lateral drift
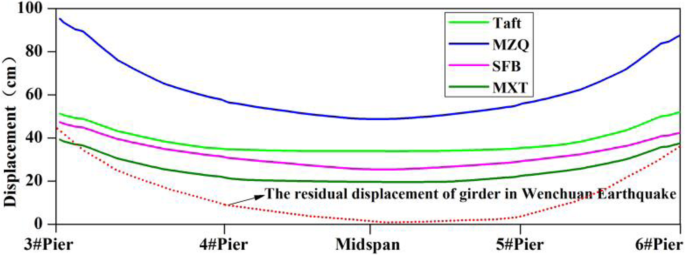
Maximum transverse displacement of Main Girde (without shear keys)
Figure 23. shows the collision-force time history of the beam end for one side span; the other side shows the similar results. When the shear keys do not fail, the maximum lateral collision force between the box girder and the shear keys exceeds 10,000 kN. Considering uplift of the beam end, the lateral collision force calculated is relatively small, about 7000 kN (Fig. 23a). The results show that the lateral collision force is large enough to damage the shear keys, which is consistent with the actual earthquake damage of the bridge. Considering uplift of the beam end, the maximum vertical collision force between the box girder and bearings is 26,000 kN, which has exceeded the vertical bearing capacity (10,000 kN) of basin rubber bearings, GPZ10SX (Fig. 23). Because the bearing pad-stone is designed according to the capacity of bearing, the pad-stone is damaged.
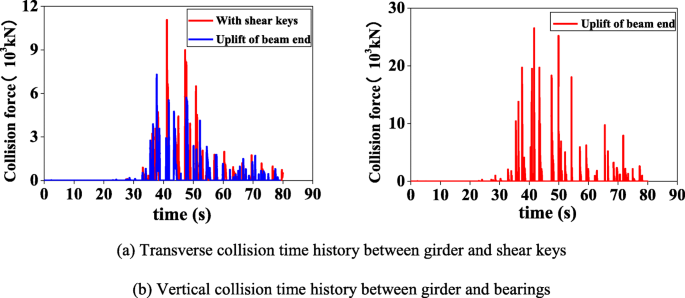
Collision time history of beam end
Control of cracking and displacement of the Main beam
Friction pendulum bearing (FPB) is widely welcomed for its simple design, effective energy consumption, and self-returning. FPB utilizes a spherical surface to contact the superstructure and substructure of the bridge. Such a surface allows sliding movement between two objects in contact, which dissipates energy through friction. The spherical profile of the contact surface also allows the superstructure to return to its balanced position under the gravity action. In this section, each transition pier is set with two FPBs on its top. The numerical model is shown in Fig. 24. The calculation of related parameters is shown in Eqs. (4)–(7).
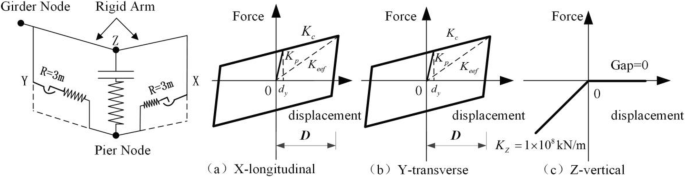
Mode of friction pendulum bearing
$$ {K}_P=\frac{\mu W}{d_y} $$
(4)
$$ {K}_{eff}=\left(\frac{1}{R}+\frac{\mu }{D}\right)W $$
(5)
$$ {K}_c=\frac{W}{R} $$
(6)
$$ F=\frac{W}{R}D+\mu W\left(\operatorname{sgn}D\right) $$
(7)
Where, R is the curvature radius of the bearing; u is the friction coefficient; d y is the yield displacement; D is the maximum value of horizontal displacement of FPB in the cyclic movement; W is the vertical load on the bearing; K p is the initial stiffness of the bearing; K eef is the equivalent stiffness of the bearing; K c is the stiffness of the bearing after yielding; F is recovery force.
Referring to the China Selection Guide for FPQZ Series Friction pendulum bearings (CCCCSHC 2013), R takes 3 m, u takes 0.05, d y takes 2.5 mm, and D takes 400 mm. Static analysis of the bridge is carried out, and the vertical reaction force W of the bearing is obtained. The initial mechanical parameters of the bearing are calculated according to Eqs. (4)–(7), as shown in Table 2.
Figure 25 shows the stress comparisons of the web under the different boundary conditions. When the FPBs are set, the principal tensile stress and principal compressive stress of the web are significantly reduced in the mid-span. Compared with the boundary conditions, i.e., that the shear keys are not damaged, FPBs can effectively reduce the principal tensile stress and principal compressive stress in the zones of the bridge girder where cracked as a result of the Wenchuan Earthquake. If the PBS is set for the bridge, there is little difference for the stress whether or not the shear keys have failed. In addition, FPBs have little effect on the web stress for the side-spans of the bridge.
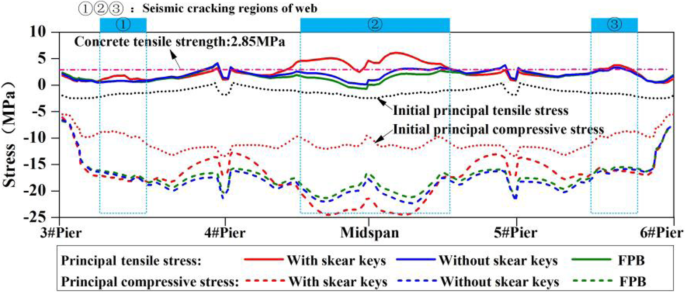
Comparison of principal tensile and principal compression stress of web
Figure 26 shows the comparison of transverse displacement response of the girder. For the side spans, the displacement reduce rates under MZQ ground motion and SFB ground motion are 31% and 24%, respectively, and those of the mid-span are − 23% and − 12%, respectively. These mean that the displacement will be amplified. Although the mid-span displacement increases to some extent, the application of FPBs can greatly reduce the lateral displacement of the side span, so as to avoid the phenomenon of side-span "residual drift". At the same time, the lateral horizontal seismic forces are evenly distributed between the side span and the middle span. In addition, the numerical simulation results show that the maximum displacement response of the FPBs under MZQ ground motion has exceeded the maximum allowable displacement D.

Transverse displacement under different boundary conditions
FPBs will slide during the strong earthquake, so the restraints are released at both ends of the beam, which also cause the loads acting on the beam to be reduced. So the response mode of the beam is more like a rigid body swing with two cantilever ends. The principal tensile stress and principal compressive stress will decrease in mid-span where cracked as a result of the Wenchuan Earthquake. Under horizontal seismic excitations, the beam end has a large horizontal displacement response. FPBs will dissipate seismic energy through friction which decrease the maximum horizontal displacement response at both ends of the beam. As a result, the deformation of the main beam is reduced, and the (principal) tensile stress is reduced as well.
Fluid viscous dampers (FVDs), another seismic resistance measure for the girder of the Miaoziping Bridge, are also discussed. Due to the limited space at the top of the transition pier, considering the actual damper layout, FVDs are only installed in the longitudinal direction of the bridge, and each transition pier is set with two FVDs. The FVD adopts the Maxwell model, and the viscous damping element is connected to an elastic connection in series. In order to simulate the pure damping effects, the smaller elastic connection stiffness K is taken, giving 1 × 107 kN/m. The bridge numerical model is shown in Fig. 27. The damping force is calculated as Eq. (8).
$$ F=C\cdot \mathit{\operatorname{sign}}\left(\dot{u}\right)\cdot {\left|\dot{u}\right|}^{\alpha } $$
(8)
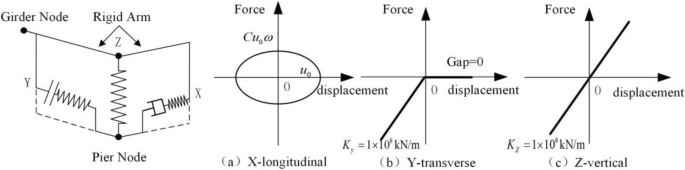
Fluid viscous damper in longitudinal direction
Where, C is the damping coefficient, taking 2000 kN·s·m− 1; α is the damping index, taking 0.5; u is relative displacement between pier and beam.
Comparison of web stress is shown in Fig. 28. The results show that the influence of the FVDs on the web stress is less than 2% and basically does not play a role in controlling this stress. The reason is that transition pier connected by the FVDs is a high pier with a small cross-section, and its longitudinal stiffness is small; whereas the stiffness of the main bridge pier is greater and is in charge of the response of the bridge. The longitudinal bending moment at the bottom of the transition pier is only 4% of the bending moment of the main pier bottom under ground motion. Longitudinal displacement of the beam end is reduced by about 10 cm after the FVDs were installed, but the bending moment at the bottom of the transition pier is doubled. These show that the structural layout of the bridge should be changed; otherwise, the isolation effects of the FVDs are few.
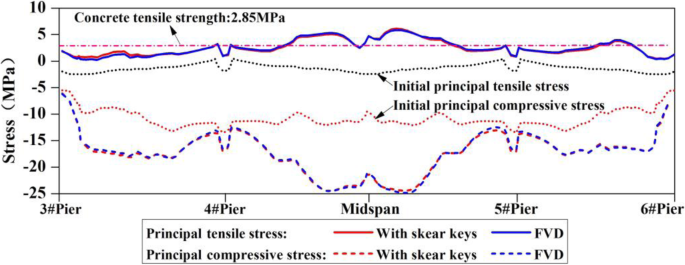
Comparison of principal tensile and principal compression stress of web
In addition, the influences of FPBs and FVDs on the stress of the bottom plate for the box section are similar to those of the web; as such, they are not discussed here.
Conclusion
To investigate the girder cracking damage of the Miaoziping Bridge in the 2008 Wenchuan earthquake, a numerical simulation of the seismic response of the main girder is carried out considering the initial stress of the box girder. Contribution of unidirectional ground motion to the stress increment of the main girder are discussed. Effects of the beam end uplift and shear keys damage on the section stress and displacement of the girder are analyzed. The seismic isolation measures of setting FPBs at the top of the transition pier are proposed. The main findings are summarized as follows:
- (1)
The girder stresses are in a full-section compression state under the serviceability case. When the bridge is subjected to three-dimensional ground motions, the girder for the rigid-frame bridge will resist the earthquake load. It bears relatively large (principal) tensile stresses. When the maximum (principal) tensile stress exceeds the tensile strength of the concrete, cracking will occur.
- (2)
The calculated high-stress distribution areas of the box girder's section are in good agreement with the real seismic damage of the bridge girder. Numerical simulation results of the Miaoziping Bridge display that the high (principal) tensile stress causes the main girder cracking. The high-tensile-stress areas of the sections include the web near the 1/6 to 1/2 length of the side-span and the middle-span length of 1/4 to 3/4, the bottom plate near the closure sections, and their adjacent two to three sections of the side span and the middle span.
- (3)
Special attention should be paid to the effect of longitudinal ground motion on the web cracking damage of the side span and middle-span. In order to control cracking and crushing of the bottom plate, attention should be paid to the effect of longitudinal ground motion on the side span, along with the effects of transverse and vertical ground motion on the mid-span. In the seismic analysis of PCCR with long spans, high piers and damaged main girder, the ground motion input must be considered in three directions.
- (4)
Considering the failure of lateral shear keys at the transition pier of the main bridge, the stress of the girder decrease in the mid-span. However, the beam ends have large lateral displacement responses. Considering uplift of the beam ends, the (principal) compressive stress and the axial torque of the side span of the girder are significantly reduced. The maximum vertical collision force between the girder and bearings exceeded the vertical bearing capacity. In general, it seems that these two types of damage behaviors are beneficial to the seismic resistance of the main girder of the bridge.
- (5)
The bi-directional FPBs are set at the top of the transition pier, which can partly reduce the principal tensile and principal compression stress of the web of the box section in the mid-span. At the same time, the large lateral displacement response of the girder of the side span at the transition pier can be controlled.
Availability of data and materials
Not applicable.
Abbreviations
- PCCR:
-
Pre-stressed concrete continuous rigid-frame bridge
- FPB:
-
Friction pendulum bearing
- FVD:
-
Fluid viscous damper
References
-
CCCCSHC (2013) China Communications Construction Company Second Highway Consultants Co.Ltd. Selection Guide for FPQZ series Friction pendulum bearings (in Chinese)
-
Chen F, Gu XY, Shan DS (2018) Seismic fragility analysis of irregular continuous rigid frame girder bridge. Cogent Eng 5(1):1–18
-
Chen LS, Zhuang WL, Zhao HQ (2012) Report on highways' damage in the Wenchuan earthquake-bridge. Beijing: China Communications Press (in Chinese).
-
Deng YL, Guo QK, Xu LQ (2019) Effects of pounding and fluid–structure interaction on seismic response of long-span deep-water bridge with high hollow piers. Arabian J Sci Eng 44(5):4453–4465
-
Ma (2008) Research on construction control of long span continuous rigid frame bridge. (MA.Eng Dissertation) Southwest Jiaotong University, P.R. China (in Chinese)
-
Guan ZG, Zhang JH, Li JZ (2017) Multilevel performance classifications of tall rc bridge columns toward postearthquake rehabilitation requirements. J Bridge Eng (ASCE) 22(10):04017080
-
Huang HD, Huang SS, Pilakoutas K (2018) Modeling for assessment of long-term behavior of Pre-stressed concrete box-girder bridges. J Bridge Eng (ASCE) 23(3):04018002 1-15
-
Jia HY, Zhang DY, Zheng SX et al (2013) Local site effects on a high pier railway bridge under tridirectional spatial excitations: nonstationary stochastic analysis. Soil Dynamics Earthquake Eng 52:55–69
-
Katsaras CP, Panagiotakos TB, Kolias B (2009) Effect of torsional stiffness of Pre-stressed concrete box girders and uplift of abutment bearings on seismic performance of bridges. Bull Earthquake Eng 7(2):363
-
Kawashima K, Takahashi Y, Ge H (2009) Reconnaissance report on damage of bridges in 2008 Wenchuan, China, earthquake. J Earthquake Eng 13(7):965–996
-
Kong XJ, Zhou Y, Zou DG et al (2012) Study of seismic wave input of Zipingpu concrete face rockfill dam during Wenchuan earthquake. Rock Soil Mech 33(7):2110–2116 (in Chinese)
-
Li XQ, Li ZX, Crewe AJ (2018) Nonlinear seismic analysis of a high-pier, long-span, continuous RC frame bridge under spatially variable ground motions. Soil Dyn Earthquake Eng 114:298–312
-
Lin YZ, Bi KM, Zong ZH et al (2020a) Seismic Performance of Steel-Concrete Composite Rigid-Frame Bridge: Shake Table Test and Numerical Simulation. J Bridge Eng (ASCE) 25(7):04020032–04021-16
-
Lin YZ, Zong ZH, Bi KM et al (2020b) Experimental and numerical studies of the seismic behavior of a steel-concrete composite rigid-frame bridge subjected to the surface rupture at a thrust fault. Eng Struct 205:110105 1-21
-
Shrestha B, Hao H, Bi KM (2015) seismic response analysis of multiple-frame bridges with unseating restrainers considering ground motion spatial variation and SSI. Adv Struct Eng 18(6):873–892
-
Sun ZG, Wang DS, Wang T (2019) Investigation on seismic behavior of bridge piers with thin-walled rectangular hollow section using quasi-static cyclic tests. Eng Struct 2019(200):1097–1110
-
Tong L, Wang DS, Wang RX (2020) Cracking damage and seismic response of large-span rigid frame bridges with high piers under strong earthquakes. Earthquake Eng Eng Vibration 40(03):108–116 (In Chinese)
-
Ucak A, Mavroeidis GP, Tsopelas P (2014) Behavior of a seismically isolated bridge crossing a fault rupture zone. Soil Dyn Earthquake Eng 57:164–178
-
Wang HL, Xie CL, Liu D et al (2019) Continuous reinforced concrete rigid-frame bridges in China. Pract Period Struct Design Construct 24(2):05019002 1-10
-
Wilson T, Chen S, Mahmoud H (2015) Analytical case study on the seismic performance of a curved and skewed reinforced concrete bridge under vertical ground motion. Eng Struct 100:128–136
-
Xu WB, Luo ZY, Yan WM et al (2020) Impact of pulse parameters on the seismic response of long-period bridges. Struct Infrastructure Eng 16(10):1461-1480
-
Yang WL, Li Q, Zhao CH (2012) Failure mechanism analysis of main bridge of Miaoziping Bridge and seismic design measures. Harbin, P.R. China (in Chinese)
-
Zong ZH, Xia ZH, Liu H et al (2016) Collapse failure of pre-stressed concrete continuous rigid-frame bridge under strong earthquake excitation: testing and simulation. J Bridge Eng (ASCE) 21(9):1–15
Acknowledgements
In this paper, the girder's crack map of the Miaoziping Bridge is mainly based on Chen et al. (2012); thanks for their hard work in the field investigation and later data publication. Thanks also to Professor Zhuang Weilin of Southwest Jiaotong University for providing the design drawings of the Miaoziping Bridge.
Funding
This work described in this paper is partially supported by the National Science Foundation of China (No. 51478074). These supports are greatly appreciated.
Author information
Authors and Affiliations
Contributions
Tong L carried out the modeling and numerical analysis. Wang DS provided guidance in methodology development and technical writing. Wang DS and Wang RX supervised and reviewed all the versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Tong, L., Wang, R. & Wang, D. Seismic cracking mechanism and control for pre-stressed concrete box girders of continuous rigid-frame bridges: Miaoziping bridge in Wenchuan earthquake as an example. ABEN 2, 17 (2021). https://doi.org/10.1186/s43251-021-00040-z
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1186/s43251-021-00040-z
Keywords
- Pre-stressed concrete continuous rigid-frame bridge
- Seismic damage
- Box girder cracking damage
- Beam end uplift
- Shear keys
- Friction pendulum bearing
Source: https://aben.springeropen.com/articles/10.1186/s43251-021-00040-z
0 Response to "Prestressed Reinforced Continuous Rigid Frame Bridge"
Post a Comment